什么是力扣二分法?
力扣二分法,又称二分查找法,是一种在有序数组中查找特定元素的算法。其核心思想是将数组分成两半,根据目标值与中间值的比较结果,决定是继续在左半部分还是右半部分查找。这种方法的时间复杂度为O(log n),在处理大量数据时效率非常高。
二分查找法的基本步骤
确定查找范围:初始化指针left指向数组的起始位置,指针right指向数组的结束位置。
计算中间位置:计算中间位置的索引mid (left + right) // 2。
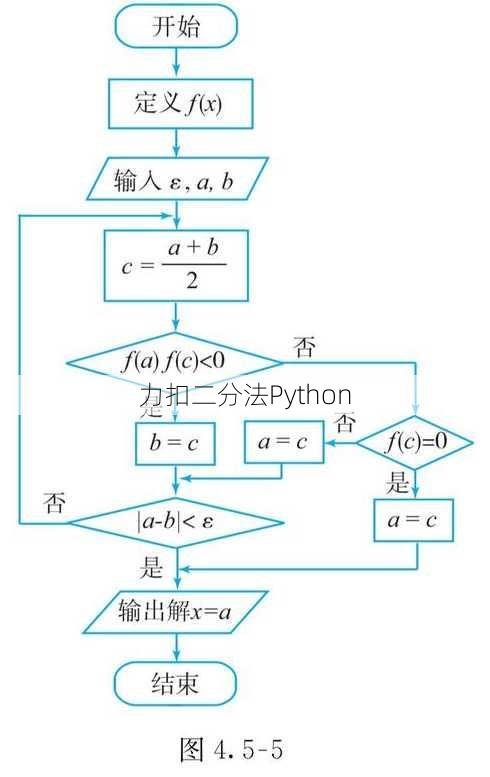
比较与调整:
如果数组中间位置的元素等于目标值,则查找成功。
如果数组中间位置的元素大于目标值,则将right指针调整到mid - 1。

如果数组中间位置的元素小于目标值,则将left指针调整到mid + 1。
- 重复步骤2和3,直到找到目标值或left大于right。
二分查找法的Python实现
以下是一个简单的二分查找法Python实现示例:
```python

def binary_search(arr, target):
left, right 0, len(arr) - 1
while left < right:
mid (left + right) // 2
if arr[mid] target:
return mid
elif arr[mid] > target:
right mid - 1
else:
left mid + 1
return -1
```
二分查找法的应用场景
有序数组查找:二分查找法适用于查找有序数组中的特定元素。
数据排序:二分查找法可以作为数据排序后的查找方法,提高查找效率。
二分图匹配:在图论中,二分查找法可以用于解决二分图匹配问题。
真实相关问题
问题一:二分查找法的时间复杂度和空间复杂度是多少?
时间复杂度:O(log n)
空间复杂度:O(1)
问题二:如何处理数组中存在重复元素的情况?
在查找过程中,可以适当调整left和right指针的范围,以确定目标元素的确切位置。
可以通过增加额外的条件判断,例如比较目标元素与相邻元素的值,以确定目标元素的位置。
问题三:二分查找法与其他查找方法的比较?
二分查找法:适用于有序数组,查找效率高,时间复杂度为O(log n)。
顺序查找法:适用于无序数组,查找效率低,时间复杂度为O(n)。
哈希表查找法:适用于任意数据结构,查找效率高,时间复杂度为O(1)。
